Pandas Correlation Between Two Columns

Pandas Correlation Between Two Columns

Correlation analysis is a vital statistical tool that helps to measure the strength and direction of the relationship between two variables. In data science, understanding the correlation between different data attributes can provide insights into the relationships within the data. Pandas, a powerful Python library for data manipulation and analysis, provides several methods to compute correlations between columns in a DataFrame. This article will explore how to calculate and interpret the correlation between two columns using Pandas, complete with detailed examples.

Understanding Correlation

Correlation coefficients range from -1 to 1. A correlation of +1 indicates a perfect positive relationship, -1 indicates a perfect negative relationship, and 0 indicates no relationship between the variables. There are several methods to calculate correlation:

• Pearson: Measures the linear relationship between two continuous variables.
• Spearman: Used for ordinal variables, based on rank correlations.
• Kendall: Similar to Spearman, but uses a different method of calculation.

Setting Up Your Environment

Before diving into the examples, ensure you have the Pandas library installed in your Python environment:

pip install pandas

Example Code Snippets

Below are detailed examples of how to calculate correlations between two columns in a DataFrame using Pandas. Each example is self-contained and can be run independently.

Example 1: Creating a DataFrame

import pandas as pd

# Sample data
data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1]
}
df = pd.DataFrame(data)
print(df)

Output:

Example 2: Calculating Pearson Correlation

import pandas as pd

data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1]
}
df = pd.DataFrame(data)
correlation = df['A'].corr(df['B'], method='pearson')
print(correlation)

Output:

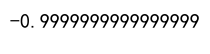
Example 3: Calculating Spearman Correlation

import pandas as pd

data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1]
}
df = pd.DataFrame(data)
correlation = df['A'].corr(df['B'], method='spearman')
print(correlation)

Output:

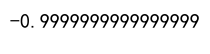
Example 4: Calculating Kendall Correlation

import pandas as pd

data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1]
}
df = pd.DataFrame(data)
correlation = df['A'].corr(df['B'], method='kendall')
print(correlation)

Output:

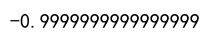
Example 5: Handling Missing Data

import pandas as pd

data = {
    'A': [1, 2, None, 4, 5],
    'B': [5, None, 3, 2, 1]
}
df = pd.DataFrame(data)
correlation = df['A'].corr(df['B'], method='pearson')
print(correlation)

Output:

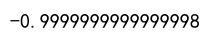
Example 6: Large Dataset Correlation

import pandas as pd
import numpy as np

# Generating large random data
np.random.seed(0)
data = {
    'A': np.random.rand(1000),
    'B': np.random.rand(1000)
}
df = pd.DataFrame(data)
correlation = df['A'].corr(df['B'])
print(correlation)

Output:

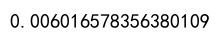
Example 7: Visualizing Correlation with Scatter Plot

import pandas as pd
import matplotlib.pyplot as plt

data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1]
}
df = pd.DataFrame(data)
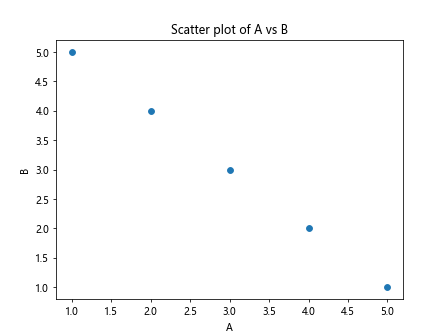
plt.scatter(df['A'], df['B'])
plt.title('Scatter plot of A vs B')
plt.xlabel('A')
plt.ylabel('B')
plt.show()

Output:

Example 8: Correlation Matrix

import pandas as pd

data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1],
    'C': [2, 3, 4, 5, 6]
}
df = pd.DataFrame(data)
correlation_matrix = df.corr()
print(correlation_matrix)

Output:

Example 9: Heatmap of Correlation Matrix

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

data = {
    'A': [1, 2, 3, 4, 5],
    'B': [5, 4, 3, 2, 1],
    'C': [2, 3, 4, 5, 6]
}
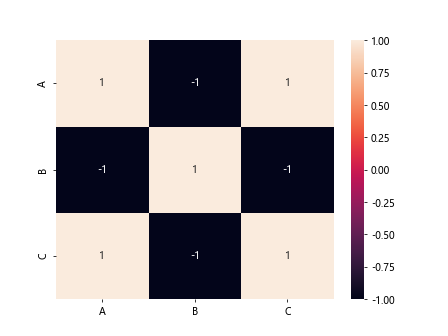
df = pd.DataFrame(data)
correlation_matrix = df.corr()
sns.heatmap(correlation_matrix, annot=True)
plt.show()

Output:

Example 10: Correlation with Categorical Data

import pandas as pd

data = {
    'A': [1, 2, 3, 4, 5],
    'B': ['low', 'low', 'high', 'high', 'medium']
}
df = pd.DataFrame(data)
df['B'] = df['B'].astype('category').cat.codes
correlation = df['A'].corr(df['B'], method='pearson')
print(correlation)

Output:

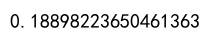
Pandas Correlation Between Two Columns Conclusion

In this article, we explored various methods to calculate the correlation between two columns using Pandas. Understanding these correlations can provide valuable insights into the relationships between variables in your data. By using the provided examples, you can start analyzing your own datasets to uncover patterns and relationships.